习题1.3第7题答案
解：∵AB⊥BD，ED⊥BD，∴∠ABC=∠EDC=90°，
又∵BC= DC， ∠ACB=∠ECD，∴△ABC≌△EDC（ASA），
∴AB=ED，∴测量DE的长就能知道A，B两点之间的距离．
习题1.3第8题答案
证明：∵BD，CE是△ABC的高，
∴∠ADB=∠AEC，∵∠A= ∠A，AB =AC，
∴△ABD≌△ACF（AAS），∴BD= CE.
习题1.3第9题答案
证明 ；∵∠:AOB=∠DOC，∠1=∠2，AB= DC，
∴△AOB≌△ DOC（AAS） ，
∴AO=DO，BO=CO，
∴AO+CO= DO+BO，即 AC= DB.
习题1.3第10题答案
证明：∵ED⊥AB， FC⊥AB，
∵∠ADE=∠BCF=90°，∵AE//BF，∵∠A=∠B．
又∵AE=BF，∴△ADE≌△BCF（AAS），
∴AD=BC，∴AD=CD=BC=CD，即AC=BD.
习题1.3第11题答案
解：（1）△ABC≌△CDA.证明：∵AB//DC，
∴∠BAC= ∠DCA. ∵AD//BC，
∴∠ACB= ∠CAD.又∵AC= CA，
∴△ABC≌△CDA （ASA）.
（2）同（1）可证得 △ABD≌△CDB.
（3）由（1）知△ABC≌△CDA，∴AB= CD.
∵∠OAB=∠OCD，∠AOB= ∠COD，
∴△ABO≌△CDO（ AAS）.
（4）同（3）理，可证得△AOD ≌△COB.
习题1.3第12题答案
解：（1）△ABC≌△AED.
证明：∵∠ACB=180°-∠3 ，∠ADE=180°-∠4，∠3=∠4，
∴∠ACB=∠ADE.又∵∠1=∠2，BC=ED，∴△ABC≌△AED（AAS）.
（2）△ABD≌△AFC.
证明：∵∠BAD=∠1+∠CAD，∠EAC=∠2+∠CAD，∠1=∠2，
∴∠BAD=∠EAC.∵BD=BC+CD，h=C=CD+DE，BC=ED，
∴BD=EC，在△ABD和△AEC中
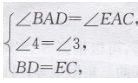
∴△ABD≌△AEC.
八年级上册物理书答案人教版
华东师大版八年级上册数学书答案
青岛版八年级上册数学书答案
人教版八年级上册英语书答案
浙教版八年级上册科学书答案
浙教版八年级上册数学书答案
人教版八年级上册语文书答案
沪科版八年级上册数学书答案
北师大版八年级上册数学书答案
人教版八年级上册数学书答案
八年级下册数学新课程自主学习与测评答案人教版
八年级下册语文同步解析与测评答案人教版
八年级下册物理同步导学与优化训练答案人教版
八年级上册地理学法大视野答案湘教版
八年级下册生物伴你学答案苏科版
人教版八年级下册英语作业本答案江西省
数学八年级上册轻轻松松学数学冀教版
北师大版八年级上册数学作业本答案江西省
人教版八年级下册生物课本答案