习题1.3第13题答案
证明 :∵AB=AC=BC，DC=DB=BC，AC=DB，
∴AB= DC.∵AE=DF，BE=CF，
∴△ABE≌△DCF（SSS） ，
∴∠A=∠D，∠ABE=∠DCF，∴AE =DF.
∵∠EBC=180°=∠ABE，∠FCB=180°∠DCF，
∴∠EBC=∠FCB，∴BE//CF.
习题1.3第14题答案
证明：∵BE= FC，BC=BE+EC，FE=FC+EC，∴BC=FE.
又∵ AC=DE，AB=DF，∴△ABC≌△DFE（SSS），
∴∠B=∠F.又 ∵∠AOB=∠DOF，AB=DF ，
∴△ABO≌△DFO（AAS），∴AODO，BO=FO.
习题1.3第15题答案
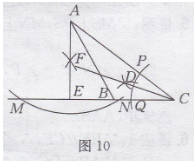
解：如图10所示，
（1）①以点C为圆心，小于BC长度为半径画圆弧，交AC于点P，交BC于点Q；
②分别以P，Q为圆心，以大于1/2PQ长度为半径画两段圆弧，使两段圆弧交于∠ACB的内部点D；
③作射线CD，则射线CD即为△ABC的角平分线．
（2）①以点A为圆心，适当长度为半径画圆弧，交直线BC于点M，N；
②分别以点M，N为圆心，以大于1/2MN长度为半径画两段圆弧，使两段圆弧交于点F；
③作直线AF，交MN于点E．则线段AE即为△ABC的高．
习题1.3第16题答案
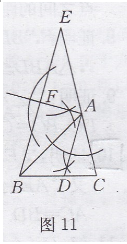
解：（1）如图11所示．
（2） EF=BF.证明如下：
∵AD平分∠BAC，∴∠BAD=∠DAC，∵∠CBE= ∠ADC，
∴AD//BE，∴∠E=∠DAC，∠ABE=∠BAD，
∴∠E= ∠ABE.∵AF//BE，∴∠AFB=∠AFE=90°，
在△AFB和△AFE中，
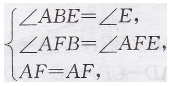
∴△AFB≌△AFE（AAS），∴EF=BF.
习题1.3第17题答案
解：∵CE⊥OA，CF⊥OB，∴△OCE和△OCF都是直角三角形．
在Rt△OCE和Rt△OCF中，
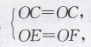
∴ Rt△OCE ≌Rt△OCF（HL），
∴∠COE=∠COF，即OC平分∠AOB.
习题1.3第18题答案
证明：∵AD是△ABC的高，
∴△ADB与△ADC都是直角三角形．
在Rt△ADB和Rt△ADC中，
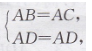
∴ Rt△ADB≌Rt△ADC（HL） ，
∴∠ DAB= ∠DAC.
∵DE⊥AB， DF⊥AC，
∴∠DEA =∠DFA.
在 △DEA和 △DFA中，
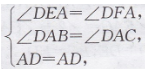
∴△DEA≌△DFA（AAS），∴DE=DF.
八年级上册物理书答案人教版
华东师大版八年级上册数学书答案
青岛版八年级上册数学书答案
人教版八年级上册英语书答案
浙教版八年级上册科学书答案
浙教版八年级上册数学书答案
人教版八年级上册语文书答案
沪科版八年级上册数学书答案
北师大版八年级上册数学书答案
人教版八年级上册数学书答案
八年级下册数学新课程自主学习与测评答案人教版
八年级下册语文同步解析与测评答案人教版
八年级下册物理同步导学与优化训练答案人教版
八年级上册地理学法大视野答案湘教版
八年级下册生物伴你学答案苏科版
人教版八年级下册英语作业本答案江西省
数学八年级上册轻轻松松学数学冀教版
北师大版八年级上册数学作业本答案江西省
人教版八年级下册生物课本答案