答案网 - 课本习题,辅导练习，辅导材料等答案解析！
语文 数学 英语
书通网logo
当前位置: 书通网 > 答案 > 九年级作业本答案 > 人教版九年级上册数学作业本答案江西省 >

人教版九年级上册数学作业本第二十一章21.2.2公式法（1）答案江西省

时间:2017-06-09 来源:书通网

第二十一章21.2.2公式法（1）第一题答案

母实数根

第二十一章21.2.2公式法（1）第二题答案

m<9/4

第二十一章21.2.2公式法（1）第三题答案

1

第二十一章21.2.2公式法（1）第四题答案

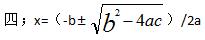
1496802540118634.jpg

第二十一章21.2.2公式法（1）第五题答案

（1）将x=1代入方程x2+ax+a-2=0，

得1+a+a-2=0，解得a=1/2，

方程为x2+1/2x-3/2=0，即2x2+x-3=0，

设另一根为x₁，则1·x₁=-3/2，x₁=-3/2

（2）∵=a2-4（a-2）=a2-4a+8=a2-4a+4+4=（a-2）2+4≥0

∴不论a取何实数，该方程有两个不相等的实数根

第二十一章21.2.2公式法（1）第六题答案

解：∵关于x的方程（k-1）x2-（k-1）x+1/4=0有两个相等的实数根，

∴△=0，

∴[-（k-1）]2-4×1/4（k-1）=0，

整理得k2-3k+2=0，

解得k₁=1（不符合一元二次方程定义，舍去），k₂=2

∴k=2

人教版九年级上册数学作业本答案江西省

更多

推荐阅读

点击查看更多内容
优美的诗句 伤感的句子 好词好句 唯美的句子 思念的诗句 经典语句

声明 :本网站尊重并保护知识产权，根据《信息网络传播权保护条例》，如果我们转载的作品侵犯了您的权利,请在一个月内通知我们，我们会及时删除。

皖ICP备11009057号